Метод Монте-Карло - это мощная статистическая техника, которая использует случайность для решения сложных задач. Названный в честь знаменитого казино Монте-Карло в Монако, этот метод стал ценным инструментом во многих областях, включая физику, финансы, инженерию и, конечно же, азартные игры.
По своей сути метод Монте-Карло предполагает многократное проведение симуляций со случайными входными данными для приближенного решения задач, которые иначе трудно вычислить. Это делает его особенно подходящим для сценариев, где исход неопределен или где многие переменные взаимодействуют непредсказуемо.
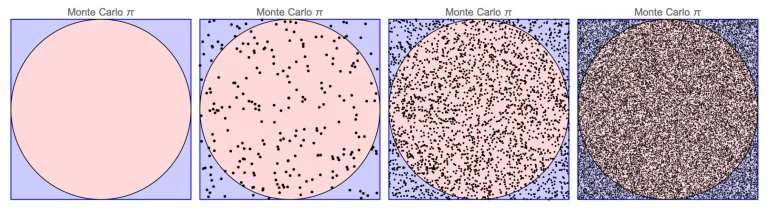
Симуляция Монте-Карло позволяет игрокам и аналитикам моделировать игры, оценивать вероятности и разрабатывать стратегии ставок в азартных играх. Он помогает ответить на многочисленніе вопросы, включая следующие:
- "Какова вероятность выигрыша с этой рукой в покере?"
- "Как стратегия ставок может проявить себя на протяжении тысяч вращений рулетки?"
Используя моделирование, имитирующее реальные сценарии азартных игр, метод Монте-Карло позволяет приблизиться к неопределенности, присущей азартным играм.
Суть метода Монте-Карло
Моделирование по методу Монте-Карло - это вычислительная техника, которая использует повторяющуюся случайную выборку для получения численных результатов.
Основная идея заключается в использовании случайности для решения задач, которые в принципе могут быть детерминированы, но слишком сложны для прямого решения. Моделируя множество сценариев, метод Монте-Карло позволяет получить оценки для широкого круга проблем, от поведения субатомных частиц до прогнозирования цен на акции.
Основной принцип метода прост: он предполагает создание модели проблемы, генерирование случайных входных данных, проведение симуляций, а затем анализ результатов. Чем больше симуляций, тем точнее аппроксимация, поскольку закон больших чисел гарантирует, что среднее значение результатов сходится к реальному значению.
Например, если вы хотите оценить вероятность выигрыша определенной руки в покере, вы можете создать модель игры, провести тысячи или даже миллионы раздач с использованием случайных входов, а затем вычислить процент случаев, когда эта рука приводит к выигрышу. Это приближенно отражает вероятность руки, даже если точный расчет слишком сложен для аналитического вычисления.
Метод Монте-Карло ценен при решении задач с большим количеством переменных или взаимодействий, когда традиционные аналитические подходы оказываются неэффективными. Вместо того чтобы решать эти проблемы с помощью прямой формулы, моделирование методом Монте-Карло разбивает сложность на управляемые симуляции, что позволяет исследовать различные исходы и сценарии.
Эта способность моделировать и симулировать сложные системы делает метод Монте-Карло универсальным инструментом в гемблинге, где случайность и вероятность играют центральную роль. Будь то оценка долгосрочных результатов стратегии ставок или расчет ожидаемой стоимости игры, метод Монте-Карло предоставляет практический способ преодоления неопределенности и принятия более обоснованных решений.
История метода Монте-Карло
Метод Монте-Карло берет свое начало в начале XX века и претерпел значительное развитие. Он получил свое название от знаменитого казино Монте-Карло в Монако.
Истоки подхода Монте-Карло восходят к развитию теории вероятностей в XVII веке. Такие математики, как Блез Паскаль и Пьер де Ферма, заложили основы для понимания случайных событий, которые впоследствии легли в основу статистических принципов, на которых основывается этот метод. Однако только в XX веке эти теоретические концепции стали применяться в практических, вычислительных контекстах.
Метод в том виде, в котором мы знаем его сегодня, появился во время Второй мировой войны, в основном благодаря работе ученых и математиков, участвовавших в Манхэттенском проекте. В частности, решающую роль в его развитии сыграли физики Станислав Улам и Джон фон Нейман. Улам начал изучать идею использования случайной выборки для решения сложных математических задач, особенно в области ядерной физики и радиации, во время выздоровления от болезни.
Концепция была формализована, когда Улам и фон Нейман разработали методику моделирования поведения частиц в различных сценариях, используя случайные числа для моделирования результатов. Эта работа заложила основу для того, что впоследствии стало методом Монте-Карло.
Улам и фон Нейман придумали название "Монте-Карло" из-за присущей этому методу зависимости от случайности, которая параллельна непредсказуемости результатов азартных игр. Ассоциация с казино Монте-Карло подчеркивала игривый и неопределенный характер создаваемых ими симуляторов.
Хотя изначально метод был разработан для научных и инженерных приложений, его принципы были восприняты и гемблерами. Игроки стали применять симуляторы Монте-Карло для анализа стратегий, оценки шансов и понимания вероятности различных исходов. Моделируя тысячи рук в покере или вращение колеса рулетки, можно получить информацию, которая поможет им принимать решения о ставках.
Сегодня симуляция Монте-Карло широко используется в различных дисциплинах, от финансов и инженерии до информатики и искусственного интеллекта. В азартных играх он по-прежнему является ценным инструментом для профессиональных игроков и случайных энтузиастов, позволяя понять стратегию и управление рисками.
Моделирование Монте-Карло в азартных играх
Метод Монте-Карло нашел свое применение в гемблинге, где случайность и вероятность - это главное. Моделируя различные исходы азартных игр, он позволяет игрокам и аналитикам получить представление о вероятностях, ожидаемой доходности и потенциальных рисках, обеспечивая более глубокое понимание того, как различные стратегии могут сыграть с течением времени.
Суть метода Монте-Карло в гемблинге заключается в использовании повторяющихся симуляций для оценки вероятностей и исходов различных игр.
Например, вместо того чтобы полагаться только на теоретические расчеты вероятности, игроки могут провести тысячи или даже миллионы симуляций игровых раундов, чтобы проследить за вероятными исходами. Такой подход помогает более точно моделировать реальные условия, включая вариации и полосы, которые трудно учесть в базовой вероятности.
Симуляторы Монте-Карло можно применять практически к любому сценарию азартных игр. Будь то вращение колеса рулетки, покер или игра на игровом автомате, этот метод позволяет азартным игрокам моделировать и анализировать возможные исходы, предоставляя оценки коэффициентов выигрыша, выплат и долгосрочной прибыльности определенных ставок.
Моделирование Монте-Карло для рулетки
Давайте рассмотрим, как метод Монте-Карло может быть применен к такой простой игре, как рулетка. В европейской рулетке есть 37 номеров: 1-36 и одно зеро. Задача состоит в том, чтобы оценить вероятность выпадения числа на красное.
- Запустив симуляцию Монте-Карло, вы можете смоделировать, скажем, 100 000 вращений виртуального колеса рулетки.
- Для каждого вращения генерируется случайное число, и если оно совпадает с красным, то это засчитывается как выигрыш.
- После завершения всех вращений доля выигрышей оценивает вероятность выпадения красного.
В результате этого процесса моделирование методом Монте-Карло показало бы, что вероятность выпадения красного в европейской рулетке составляет примерно 48,65 %, что полностью соответствует истинной теоретической вероятности. Этот метод особенно полезен при попытке понять, как определенные стратегии ставок могут работать на протяжении многих спинов, помогая оценить риски и потенциальную выгоду.
| Название | Софт | Процент выплаты | |||
|
|
98.65% | Играть | |||
|
|
98.65% | Играть | |||
|
|
98.65% | Играть | |||
|
|
98.65% | Играть | |||
|
|
98.65% | Играть | |||
|
|
98.6% | Играть | |||
|
|
98.05% | Играть | |||
|
|
97.3% | Играть | |||
|
|
97.3% | Играть | |||
|
|
97.3% | Играть |
Моделирование Монте-Карло для покера
В покере игрокам часто требуется рассчитать вероятность выигрыша с определенной рукой против потенциальных оппонентов. Для оценки вероятности различных исходов можно использовать симуляцию Монте-Карло. Например, в техасском холдеме вам может понадобиться узнать вероятность выигрыша с парой тузов против ряда возможных рук.
Запустив симуляцию Монте-Карло, вы можете смоделировать тысячи рук с различными картами борда и рассчитать, как часто пара тузов будет выходить на первое место. Симуляция может предоставить вероятность выигрыша на основе всех возможных сценариев, помогая игроку принимать лучшие решения о том, когда делать ставку, повышать или фолдить.
Эти примеры иллюстрируют, как метод Монте-Карло позволяет азартным игрокам выйти за рамки интуиции или базовой стратегии, используя данные для обоснования своего игрового процесса.
Применение для гемблеров
Метод Монте-Карло - это не только инструмент для случайных игроков; он также ценен для адвантивных гемблеров - тех, кто использует различные техники, чтобы склонить шансы в свою пользу. Такие игроки полагаются на глубокое понимание вероятности, стратегии и риска, а метод Монте-Карло дает им возможность усовершенствовать свои подходы с помощью детального моделирования.
Вот несколько ключевых применений метода Монте-Карло для игроков с преимуществом.
Подсчет карт в блэкджеке
Одна из самых известных техник игры с преимуществом - подсчет карт в блэкджеке. Отслеживая сданные карты, счетчики карт могут оценить вероятность появления определенных карт в предстоящих раздачах и, соответственно, скорректировать свои ставки и стратегию игры. Метод Монте-Карло помогает в этом процессе, моделируя тысячи игр в блэкджек при различных условиях.
Например, игрок может использовать симуляторы Монте-Карло, чтобы увидеть, как подсчет карт влияет на вероятность выигрыша в различные моменты. Они могут моделировать сценарии с различными подсчетами и стратегиями ставок, чтобы найти оптимальный подход. Моделирование поможет ответить на вопросы типа "Какова ожидаемая прибыль, если я удвою ставку при счете +2?". Проводя такие симуляции, карточные игроки могут точно настроить свою стратегию, чтобы максимизировать прибыль и минимизировать риски.
| Название | Софт | Процент выплаты | ||
|
|
99.92% | |||
|
|
99.91% | |||
|
|
99.87% | |||
|
|
99.78% | |||
|
|
99.71% | |||
|
|
99.7% | |||
|
|
99.69% | |||
|
|
99.65% | |||
|
|
99.63% | |||
|
|
99.63% |
Стратегии ставок и управление банкроллом
Симуляции Монте-Карло также являются ценным инструментом для тестирования различных стратегий ставок. Такие распространенные стратегии, как система Мартингейла или критерий Келли, основаны на корректировке размеров ставок в зависимости от выигрышей и проигрышей. Но прежде чем использовать эти стратегии в реальных играх, гемблеры часто хотят понять их долгосрочные последствия, особенно в отношении управления банкроллом.
С помощью метода Монте-Карло игроки могут смоделировать тысячи сессий ставок, каждый раз применяя ту или иную стратегию. Это позволяет им увидеть влияние на свой банкролл с течением времени, включая полосы выигрышей и проигрышей. Например, если игроки хотят проверить, как стратегия Мартингейла работает в рулетке, они могут смоделировать серию ставок с разными исходами. Это поможет выявить возможность значительных колебаний банкролла и риск остаться без денег во время полосы неудач.
Игроки могут лучше понять баланс между риском и вознаграждением, моделируя различные стратегии ставок и принимая обоснованные решения о том, сколько ставить, когда остановиться и каких стратегий избегать. Например, они могут обнаружить, что стратегия Мартингейла, хотя и заманчива, но несет в себе значительный риск быстрого истощения средств в случае проигрыша, в то время как критерий Келли может обеспечить более сбалансированный подход к управлению рисками.
Моделирование результатов игры для поиска оптимальной стратегии
Адвантивные гемблеры часто сосредотачиваются на поиске оптимальной стратегии для конкретной игры или сценария, и метод Монте-Карло может помочь в этом поиске. Например, в видеопокере игрокам необходимо решить, какие карты оставить, а какие сбросить, исходя из ожидаемой стоимости каждого решения. Помочь в этом может симуляция Монте-Карло, которая позволяет смоделировать все возможные исходы для различных вариантов и сравнить их ожидаемые значения.
Таким образом, игроки могут определить, какие варианты максимизируют их шансы на выигрыш с течением времени. С помощью этого метода можно рассчитать долгосрочное ожидание каждого возможного события, что дает основу для принятия оптимальных решений, подкрепленную данными. Этот подход не ограничивается покером, он может быть применен и к другим играм, основанным на навыках, таким как блэкджек, баккара или даже к конкретным сценариям спортивных ставок.
Эти приложения демонстрируют, как метод Монте-Карло позволяет адвантивным гемблерам глубже изучить динамику игры, проверить теории и найти преимущества, которые случайные игроки могут упустить.
Инструменты для моделирования симуляций Монте-Карло
В то время как метод Монте-Карло можно применять вручную, имея достаточно времени и терпения, использование специализированных инструментов и программного обеспечения может значительно упростить процесс, облегчая быстрое и точное проведение масштабных симуляций. Многие из этих инструментов доступны как новичкам, так и опытным пользователям, позволяя игрокам с легкостью анализировать сложные сценарии.
Ниже представлен обзор популярных инструментов и программного обеспечения для проведения симуляций Монте-Карло в азартных играх.
- Excel с VBA (Visual Basic for Applications) - широко распространенный инструмент для создания простых симуляторов Монте-Карло, особенно в сочетании с VBA. VBA позволяет автоматизировать процесс моделирования путем написания небольших программ для генерации случайных чисел и отслеживания результатов. Excel идеально подходит для моделирования простых азартных игр, таких как подбрасывание монет, броски костей или базовые карточные игры. Его также можно использовать для моделирования стратегий ставок, автоматизируя расчеты выигрышей, проигрышей и корректировки банкролла.
- Python - универсальный язык программирования, популярный для анализа данных и моделирования. В нем есть такие библиотеки, как NumPy для генерации случайных чисел и Pandas для манипулирования данными, что делает его отличным выбором для проведения симуляций Монте-Карло. Python может выполнять сложные симуляции, такие как расчет вероятностей покерных рук, моделирование стратегий игры в рулетку или симуляция тысяч спинов на игровых автоматах. Он особенно полезен при работе с большими массивами данных или при необходимости моделирования нескольких сценариев.
- R - это язык статистического программирования, который отлично справляется с анализом данных и визуализацией, что делает его отличным выбором для моделирования методом Монте-Карло. R хорошо подходит для моделирования сценариев, требующих особого внимания к статистическому анализу, например, для анализа дисперсии различных стратегий ставок или расчета ожидаемой стоимости в сложных карточных играх.
- @RISK, Simul8 и другие специализированные пакеты также пригодны для подобного моделирования. Они имеют встроенные функции для создания симуляций, генерации случайных переменных и анализа результатов. С их помощью можно тестировать сложные системы ставок, проводить тысячи симуляций игр и создавать подробные отчеты.
- Онлайн-симуляторы и калькуляторы позволяют запускать эксперименты данного рода прямо в браузере, не загружая программное обеспечение и не составляя код. Онлайн-симуляторы могут стать отличным способом быстрого анализа простых игр, таких как броски костей, подбрасывание монет или розыгрыш рук в блэкджеке. Часто они имеют предопределенные настройки и модели для популярных азартных игр.
Эти инструменты и программное обеспечение позволяют азартным игрокам эффективно проводить симуляцию Монте-Карло для анализа своих игр и стратегий.
Плюсы и минусы метода Монте-Карло в гемблинге
Хотя метод Монте-Карло является мощным инструментом для анализа и моделирования сценариев азартных игр, у него есть свои сильные и слабые стороны. Понимание этих преимуществ и ограничений крайне важно для азартных игроков, которые хотят эффективно использовать этот метод для улучшения своих стратегий и принятия решений.
Преимущества
- Допускает моделирование сложных сценариев. Одним из самых больших преимуществ метода Монте-Карло является его способность моделировать сложные системы, в которых множество переменных взаимодействуют непредсказуемым образом. В азартных играх можно моделировать даже игры с запутанными правилами и множеством возможных исходов, например покер или ставки на спорт, чтобы оценить различные вероятности и исходы.
- Позволяет тестировать стратегии. Метод Монте-Карло позволяет игрокам тестировать различные стратегии ставок, прежде чем вкладывать реальные деньги. Например, игрок может смоделировать , как система Мартингейла или Пароли будет работать в тысячах игр, что поможет ему понять потенциальные риски и вознаграждения без необходимости испытывать их в реальных условиях казино.
- Помогает в управлении рисками. Моделируя широкий спектр сценариев, метод Монте-Карло дает игрокам более четкое представление о возможных рисках и о том, как эти риски могут повлиять на их банкролл. Например, игроки могут оценить шансы попасть в полосу неудач, которая может истощить их банкролл, что позволяет им планировать более безопасные суммы ставок.
- Дает представление о математическом ожидании. Ожидаемое значение (EV) - важнейшее понятие в азартных играх, представляющее собой средний результат конкретной ставки за определенное время. Метод Монте-Карло помогает оценить EV различных ставок или рук в таких играх, как блэкджек или покер, подсказывая игрокам, как играть - агрессивно или консервативно, исходя из рассчитанного преимущества.
- Помогает принимать долгосрочные решения. Поскольку метод Монте-Карло позволяет моделировать тысячи или миллионы игровых раундов, он помогает игрокам понять долгосрочную эффективность своих стратегий. Это особенно полезно в играх с низким хаус эджем, где долгосрочное поведение ставок может значительно отличаться от краткосрочных результатов.
Ограничения
- Проведение симуляций Монте-Карло может потребовать значительных вычислительных мощностей, особенно при моделировании сложных игр с большим количеством переменных. Например, моделирование миллионов покерных рук с различными стратегиями игроков может потребовать значительного времени обработки даже на современных компьютерах.
- Хотя моделирование методом Монте-Карло позволяет получить оценки и вероятности, оно не гарантирует результат. Результаты основаны на выборке возможных сценариев, а значит, на них может повлиять случайность, присущая каждой симуляции. Поэтому иногда результаты моделирования могут отличаться от теоретических вероятностей.
- Точность симуляции Монте-Карло в значительной степени зависит от качества используемой модели. Например, если в покерной симуляции не учитывается, как играют или блефуют соперники, полученные вероятности могут ввести в заблуждение. Это означает, что игроки должны хорошо понимать игру, которую они моделируют, чтобы построить точные симуляции.
- В то время как метод Монте-Карло отлично подходит для анализа долгосрочных вероятностей, он менее эффективен для понимания краткосрочных тенденций или полос, на которые часто обращают внимание многие азартные игроки. Например, он может не предсказать, когда закончится полоса неудач или когда произойдет следующий выигрыш в таких играх, как слоты.
- Эффективное использование метода Монте-Карло требует базового понимания вероятности, статистики и программирования (при использовании таких инструментов, как Python или R). Для некоторых игроков обучение может оказаться слишком сложным, что затруднит использование этого метода без вложения времени в освоение базовых концепций.
Взвесив все преимущества и ограничения, игроки могут решить, когда и как использовать метод Монте-Карло для улучшения своего понимания игр.
Применение метода Монте-Карло в играх казино
Чтобы понять практическое применение метода Монте-Карло в азартных играх, полезно рассмотреть конкретные примеры в популярных играх казино.
Блэкджек: расчет матожидания базовой стратегии
Игрок хочет узнать математическое ожидание (EV) определенной стратегии игры в блэкджек, например, всегда брать карту на мягких 17 или удваиваться на определенных руках. Метод Монте-Карло позволяет игроку смоделировать тысячи раундов игры в блэкджек с использованием этой стратегии, чтобы увидеть, как она работает с течением времени.
Игрок создает виртуальную колоду карт и пишет программу (или использует программное обеспечение), которая раздает карты в соответствии с правилами блэкджека, моделирует выбранную стратегию и записывает результаты каждого раунда. Этот процесс повторяется в течение 100 000 или более рук.
В ходе моделирования рассчитывается процент выигранных, проигранных или запущенных рук, а также общая рентабельность инвестиций (ROI) в стратегию. Например, игрок может обнаружить, что попадание в мягкие 17 приводит к более низкой долгосрочной прибыли по сравнению со стоянием. Полученные данные помогут игроку выбрать наиболее выгодную стратегию в будущих играх.
Покер: моделирование вероятностей рук
В техасском холдеме игрок хочет оценить свои шансы на победу с парой королев против двух других оппонентов с неизвестными руками. Вместо того чтобы полагаться на таблицы покерных коэффициентов, они используют метод Монте-Карло, чтобы смоделировать тысячи игр с различными возможными руками противников.
Игрок создает программу, которая случайным образом генерирует карты сообщества и возможные руки соперников для каждой симулируемой игры. Результат записывается для каждого запуска, чтобы определить, выигрывает ли пара королев, ничья или проигрывает.
После моделирования 1 000 000 рук игрок видит, что его пара королев выигрывает примерно в 65 % случаев против двух случайных оппонентов. Это поможет игроку решить, что делать: коллировать, повышать или фолдить в реальных игровых ситуациях, основываясь на расчетной вероятности выигрыша.
Рулетка: тестирование системы ставок
Игрок хочет оценить систему ставок Мартингейла в европейской рулетке, при которой он удваивает ставку после каждого проигрыша и обнуляет ее после выигрыша. Игрок хочет знать, каков риск банкротства и как стратегия работает в течение длительных сессий.
Имитационная установка: Используя метод Монте-Карло, игрок моделирует 100 000 сессий по 200 спинов в каждой, начиная с определенного банкролла и применяя стратегию Мартингейла. Каждая сессия заканчивается, когда игрок либо достигает цели по прибыли, либо у него заканчиваются деньги.
Моделирование показало, что, хотя система Мартингейла позволяет часто получать небольшие выигрыши, существует значительный риск попасть в длительную полосу неудач, которая быстро истощит банкролл игрока. Результаты показывают, что ожидаемый результат стратегии с течением времени становится отрицательным из-за преимущества дома, что делает ее рискованной для длительной игры. Это позволяет игроку понять опасность использования такой системы.
Игровые автоматы: понимание волатильности
Игроку интересно понять волатильность конкретной игры на игровом автомате. Он хочет оценить, как часто он может сорвать джекпот или испытать длительную полосу проигрышей.
Игрок использует симуляцию Монте-Карло, чтобы воспроизвести таблицу выплат игрового автомата и смоделировать миллионы спинов, при этом каждый спин случайным образом определяет результаты, основанные на RTP (Return to Player) автомата и частоте выпадений.
Симуляция дает подробную информацию о том, как часто происходят различные выплаты, о типичной длине полос выигрышей и проигрышей, а также о среднем времени между выпадениями джекпотов. Это помогает игроку определить, соответствует ли игра его предпочтениям в отношении риска и вознаграждения, например, предпочитает ли он частые небольшие выигрыши или шанс на более крупные выплаты.
Эти примеры демонстрируют, насколько универсальным и мощным может быть метод Монте-Карло для азартных игроков.
| Название | Процент выплаты | Максимальное умножение | Вариативность | Софт | ||
| 99.07% | x1000 | Низкая |
|
Играть | ||
| 99% | x12075 | Высокая |
|
Играть | ||
| 98.98% | x3843 | Средняя |
|
Играть | ||
| 98.72% | — | — |
|
Играть | ||
| 98.67% | — | — |
|
Играть | ||
| 98.6% | x670 | Низкая |
|
Играть | ||
| 98.18% | — | Низкая |
|
Играть | ||
| 98.13% | x15000 | Высокая |
|
Играть | ||
| 98.12% | x500 | Низкая |
|
Играть | ||
| 98.12% | x2064 | Средняя |
|
Играть | ||
| 98.12% | x10000 | Высокая |
|
Играть | ||
| 98.11% | x7500 | — |
|
Играть | ||
| 98.11% | x100 | Средняя |
|
Играть | ||
| 98.11% | x1500 | Высокая |
|
Играть | ||
| 98.1% | x2500 | — |
|
Играть |
Советы по использованию метода Монте-Карло
Чтобы извлечь максимальную пользу из метода Монте-Карло, игрокам важно применять его вдумчиво. Вот несколько практических советов, как эффективно использовать этот метод, чтобы симуляции были точными, проницательными и соответствовали реальным сценариям.
1. Начните с четких целей
- Прежде чем проводить симуляцию, четко определите, чего вы хотите добиться. Проверяете ли вы долгосрочную прибыльность системы ставок, оцениваете дисперсию конкретной игры или понимаете риск разорения при определенном размере банкролла? Четкая цель гарантирует, что симуляция будет разработана правильно и что вы сосредоточитесь на соответствующих данных.
- Определите, какие переменные наиболее важны для вашей симуляции, например шансы на выигрыш, размер ставки, правила игры или продолжительность сессии. Сосредоточение на этих критических факторах сделает симуляцию более эффективной и позволит вам не тратить время на моделирование ненужных деталей.
2. Используйте реалистичные исходные данные
- Точность моделирования методом Монте-Карло зависит от качества данных, которые вы используете. Если вы моделируете покерные руки, используйте реалистичные распределения карт и вероятности. Для ставок на спорт используйте реальную игровую статистику и данные о результатах игроков. Чем реалистичнее исходные данные, тем надежнее результаты.
- Учитывайте математическое превосходство заведения. При моделировании игры в казино всегда учитывайте хаус эдж в своих расчетах. Это встроенное преимущество, которое казино имеет перед игроком. Учитывание House Edge поможет вам лучше отразить реальные результаты и понять, как это преимущество влияет на вашу стратегию.
3. Проведите достаточное количество симуляций
- Проведение всего нескольких симуляций может привести к результатам, искаженным случайными факторами. Чтобы получить достоверную оценку, необходимо провести тысячи или даже миллионы итераций, в зависимости от сложности игры и количества переменных. Больший объем выборки дает более точное представление о возможных результатах и уменьшает влияние выбросов.
- Отследите, стабилизируются ли результаты моделирования по мере увеличения числа итераций. Например, если вы оцениваете процент выигрыша покерной руки, процентное соотношение должно стабилизироваться около определенного значения по мере увеличения количества смоделированных рук. Это указывает на то, что моделирование достигло надежного результата.
4. Интерпретируйте результаты с осторожностью
- Поймите, что такое изменчивость. Даже при большом количестве симуляций результаты метода Монте-Карло отражают распределение возможных исходов, а не точные прогнозы. Имейте в виду, что краткосрочные результаты в реальных игровых сессиях могут значительно отличаться от смоделированного среднего значения.
- При анализе результатов моделирования используйте доверительные интервалы, чтобы понять, в какой диапазон могут попасть результаты. Это поможет вам понять потенциальную вариативность и не придавать слишком большого значения оценке по одному пункту.
5. Сосредоточьтесь на долгосрочном анализе
- Результаты азартных игр могут быть очень изменчивы в краткосрочной перспективе, поэтому использование метода Монте-Карло для моделирования более длительных периодов - например, тысяч спинов или рук - позволяет получить более четкое представление о долгосрочной жизнеспособности стратегии. Это особенно важно для понимания таких игр, как блэкджек, где небольшие преимущества накапливаются с течением времени.
- Используйте симуляцию, чтобы предугадать, как ваш банкролл может меняться со временем. Например, понимание вероятности серии проигрышей поможет вам установить более реалистичные лимиты банкролла и избежать преждевременного исчерпания средств.
6. Сочетайте Монте-Карло с другими аналитическими методами
- Симуляции Монте-Карло - это лишь одна из составляющих набора инструментов азартного игрока. Сочетание их с другими статистическими методами, такими как регрессионный анализ или проверка гипотез, может дать более полное представление об игре или стратегии. Например, после проведения симуляции вы можете проанализировать результаты, чтобы определить, какие переменные в наибольшей степени влияют на исход.
- После проведения симуляции сравните результаты с известными теоретическими вероятностями для изучаемой игры. Это поможет убедиться в том, что ваша симуляция работает правильно и соответствует ожидаемым вероятностям, а также послужит проверкой разумности вашей модели.
7. Не забывайте о времени и вычислительных ресурсах
- Если вы проводите моделирование на домашнем компьютере или с помощью простого программного обеспечения, подумайте о том, как оптимизировать код или модель, чтобы сократить время вычислений. Это может включать упрощение вычислений, уменьшение количества отслеживаемых переменных или использование более эффективных алгоритмов.
- Если вам нужно провести особенно крупные или сложные моделирования, использование облачных вычислений может ускорить процесс. Многие облачные платформы позволяют арендовать вычислительные мощности по мере необходимости, что упрощает работу с большими массивами данных, необходимыми для детального анализа методом Монте-Карло.
8. Учитесь у других гемблеров
- Существует множество онлайн-сообществ, в которых игроки и любители данных делятся своим опытом работы с симуляторами Монте-Карло. На таких сайтах, как GitHub, Stack Overflow, и специализированных форумах по азартным играм часто можно найти примеры кода, обсуждения и стратегии, которые помогут вам усовершенствовать свои собственные симуляции.
- Многие опытные игроки публикуют свои анализы или пишут о своих подходах к использованию симуляторов Монте-Карло в книгах, блогах или статьях. Изучение этих ресурсов может предложить новые идеи и методы, которые вы, возможно, не рассматривали, что поможет вам улучшить свои собственные симуляции.
Такой подход позволяет лучше подготовиться, глубже понять и получить стратегическое преимущество как в играх казино, так и в ставках на спорт, что в конечном итоге позволяет максимально эффективно использовать этот мощный математический инструмент.
Заключительные размышления
Метод Монте-Карло - это мощная основа для гемблеров, которые стремятся улучшить понимание риска, вероятности и стратегии в различных сценариях азартных игр. Используя этот метод, они могут моделировать бесчисленное количество исходов, оценивать эффективность различных стратегий и принимать решения, основанные на данных, которые могут привести к улучшению результатов за столами или во время ставок на спорт.
В заключение следует отметить, что метод Монте-Карло - это не просто математическая техника; это мощный союзник для игроков, стремящихся разобраться в тонкостях своей игры.
Используя этот метод, игроки могут улучшить процесс принятия решений, эффективнее управлять рисками и в конечном итоге получить более стратегический и осознанный опыт игры. Как и в случае с любым другим инструментом, главное - понять его применение и грамотно использовать, чтобы ориентироваться в захватывающем и непредсказуемом мире азартных игр.